Pair of Tangents, Chord of Contact and Chord with Midpoint of a Circle

The angle between the tangents drawn from origin to the circle ${\left(x-7\right)}^2+{\left(y+1\right)}^2=25$ is equal to____.

The equation of circle such that the length of the tangent to it from the points $(1,0),\left(2,0\right)$ and $\left(3,2\right)$ are $1,$ $\sqrt{7}\text{,} \sqrt{2}$ respectively, is

Let $2{\text{x}}^2+{\text{y}}^2-3\text{xy}=0$ be the equation of a pair of tangents drawn from the origin 'O' to a circle of radius 3 with centre in the first quadrant. If A is one of the points of contact, find the length of OA.

Consider a circle S with centre at the origin and radius $4$. Four circles $A, B, C$ and $D$ each with radius unity and centres $\left(-3,0\right), \left(-1,0\right), \left(1,0\right)$ and $\left(3,0\right)$ respectively are drawn. $A$ chord $PQ$ of the circle $S$ touches the circle $B$ and passes through the centre of the circle $C$. If the length of this chord can be expresses as $\sqrt{x}$, find $x$.

The area of the triangle formed by the tangents from the point $(4, 3)$ to the circle $x^2+y^2=9$ and the line joining their points of contact is

Let $x^2+y^2-4x-2y-11=0$ be a circle. A pair of tangents from the point $(4, 5)$ with a pair of radii form a quadrilateral of the area:

$x^2+y^2-4x-2y-11=0$ is a circle to which tangents are drawn from the point $\left(4,5\right)$ which form a quadrilateral with a pair of radii. The area of this quadrilateral in square units is ___________.

The points at which two circles with unequal radii subtend equal angles lies on

Let $A$ be the centre of the circle $x^2+y^2-2x-4y-20=0,$ and $B\left(1,7\right)$ and $D(4,-2)$ are points on the circle then, if tangents be drawn at $B$ and $D$, which meet at $C$, then area of quadrilateral $ABCD$ is

If $P$ is a point such that the ratio of the squares of the lengths of the tangents from $P$ to the circles $x^2+y^2+2x-4y-20=0$ and $x^2+y^2-4x+2y-44=0$ is $2:3$, then the locus of $P$ is a circle with centre

The distance between the chords of contact of tangents to the circle $x^2+y^2+2gx+2fy+c=0$ from the origin and the point $(g, f)$ is :

Find the equation of the chord of the circle $x^2+y^2-8x+2y+1=0$, whose middle point is $\left(5, 2\right)$.

The locus of the mid points of the chords of the circle $x^2+y^2-2bx=0$ passing through the origin is

$AP, AQ$ and $BC$ are tangents on the circle, as shown in figure. If $AB=3 cm$, $AC=4 cm, BC=6 cm$ and $AP=L cm$, then value of $(4L+5)$ is

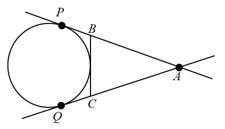
If $A$ and $B$ are the point of contact of pair of tangents drawn from $P\left(6,8\right)$ on the circle $x^2+y^2=16$, then the circumradius of $\Delta OAB$ (where $O$ being origin) is

Let $T$ be a circle with diameter $AB$ and centre $O$. Let $l$ be the tangent to $T$ at $B$. For each point $M$ on $T$ different from $A$, consider the tangent $t$ at $M$ and let interest $l$ at $P.$ Draw a line parallel to $AB$ through $P$ intersecting $OM$ at $Q.$ The locus of $Q$ as $M$ varies over $T$ is

If $P\left(x_1,y_1\right)$ is a point such that the lengths of the tangents from it to the circles $x^2+y^2-4x-6y-12=0$ and $x^2+y^2+6x+18y+26=0$ are in the ratio $2:3$, then the locus of $P$ is

If the lengths of the tangents drawn from $P$ to the circles $x^2+y^2-2x+4y-20=0$ and $x^2+y^2-2x-8y+1=0$ are in the ratio $2:1$, then the locus of $P$ is

If the chord of contact of tangents from a point $A$ to a given circle passes through $B$, then the circle with $AB$ as a diameter will